English

О ширине запрещенной зоны твердых тел (база данных "Bandgap")

Цитирование

Если Вы используете БД "Bandgap" в научных работах мы будем признательны Вам за цитирование следующей статьи:

Киселева Н.Н., Дударев В.А., Коржуев М.А. База данных по ширине запрещенной зоны неорганических веществ и материалов // Материаловедение. 2015. №7. С. 3-8.

Введение

Понятие запрещенной зоны E_g (или энергетической щели в электронном спектре ΔE) кристалла возникло в физике твердого тела в процессе объяснения различий физических свойств металлов и диэлектриков в рамках квантовой теории [1]. Согласно представлениям квантовой теории при образовании кристалла из отдельных атомов вследствие уменьшения межатомных расстояний и действия принципа Паули происходит размытие дискретных электронных уровней атомов в квазинепрерывные разрешенные зоны (полосы), имеющие определенную протяженность по шкале энергий. Разрешенные зоны кристалла разделяются запрещенными зонами, плотность электронных состояний в которых равна нулю [1-6].

Электроны заполняют только разрешенные зоны. В запрещенных зонах идеального кристалла электроны располагаться не могут [2,3]. При этом число конечных электронных состояний в разрешенных зонах кристалла точно соответствует числу исходных состояний в образующих его атомах [4]. Для характеристики заполнения электронных зон вводят понятие энергии (уровня) Ферми E_F, отделяющей на шкале энергий заполненные электронные состояния кристалла от свободных при нулевой абсолютной температуре (Т = 0 К).

Соответственно в зависимости от положения уровня Ферми E_F на шкале энергий разрешенные зоны кристалла могут заполняться электронами полностью, частично, либо оставаться незаполненными. Верхняя из заполненных электронами зон называется валентной зоной, нижняя из незаполненных - зоной проводимости [3].

Расположение уровня Ферми E_F относительно краев указанных зон определяет электронную природу и физические свойства кристалла. Действительно, валентные электроны кристалла, находящиеся в заполненных зонах, являются связанными и не участвуют в проводимости. Электроны могут стать свободными и участвовать в электронной проводимости только в том случае, если они находятся в незаполненной зоне [4]. Соответственно вещества, в которых валентная зона заполнена частично, либо зона проводимости и валентная зоны перекрываются, являются металлами (электроны при этом дополнительно не должны быть локализованы). Вещества, в которых при нулевой абсолютной температуре (Т = 0 К) валентная зона и зона проводимости не перекрываются, являются полупроводниками или диэлектриками [3,4].

Динамические характеристики электронов в зоне проводимости определяются зависимостями их энергии E от квазиимпульса p=(h/2π)k (здесь k - волновой вектор). Обычно дисперсионные соотношения E=f(p) вблизи краев зон описываются квадратичными зависи-мостями:

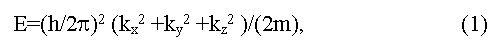
(здесь h- постоянная Планка, k_i - пространственные компоненты волнового вектора, m - эффективная масса носителей тока), а вдали от экстремумов приобретают более сложный вид [5,6]. Общая картина зонной структуры кристалла в координатах E-k представляет собой набор дисперсионных кривых, энергетические зазоры между которыми меняются по абсолютной величине от точки к точке в пространстве квазиимпульса [6]. Пространственная периодичность кристалла определяет периодичность пространства квазиимпульса (скоростей) электронов, что позволяет выделить в обратном пространстве элементарную ячейку, называемую зоной Бриллюена. Форма зоны Бриллюена определяется симметрией кристалла, при этом энергетические экстремумы на дисперсионных кривых достигаются обычно в симметричных точках зоны Бриллюена (L, X, Δ, Γ и других).

Запрещенная зона E_g и химическая связь в твердых телах

Природу химической связи в материале в значительной степени определяет минимальный энергетический зазор между абсолютным максимумом валентной зоны и абсолютным минимумом зоны проводимости, который называют фундаментальной запрещенной зоной, или просто запрещенной зоной кристалла E_g [1,5]. В зависимости от того, располагаются ли экстремумы зоны проводимости и валентной зоны в одних и тех же точках, либо разнесены в пространстве квазиимпульса, запрещенная зона E_g называется прямой или непрямой [4,5].

Полупроводники и диэлектрики различаются величиной E_g. Условно вещества с E_g > 2-3 eV (1 eV= 1.6021*10^-12 Эрг = 1.6021*10^-19 Дж) относят к классу диэлектриков, вещества с E_g < 2-3 eV - к классу полупроводников. (1.5 eV < Eg < 2-3 eV - к классу широкозонных полупроводников, E_g < 0.1- 0.2 eV - к классу узкозонных полупроводников), вещества с E_g ≈ 0 - к классу бесщелевых полупроводников, вещества с E_g ≤ 0 (небольшое перекрытие зон) - к классу полуметаллов. К полуметаллам относятся также сильнолегированные полупроводники с металлическим характером проводимости, уровень Ферми в которых расположен глубоко в зонах проводимости, либо в валентной зоне [5,7].

Понятие E_g может быть распространено также на разупорядоченные и сильно дефектные фазы, в том числе на аморфные тела (стекла) [8,9], а также жидкости [10], где роль E_g играет квазищель E_g*. Последняя представляет собой энергетический зазор в электронном спектре, вблизи краев которого, а также и в его глубине, могут присутствовать как локализованные, так и распространенные электронные состояния.

При переходе к газообразным диэлектрическим фазам понятие E_g теряет смысл (по крайней мере, при давлениях, отличных от сверхвысоких), трансформируясь в расстояние между занятыми и свободными уровнями энергии электронов в атомах или молекулах.

Таким образом, E_g является фундаментальным параметром конденсированных фаз, который характеризует природу химической связи в материале.

E_g материалов и ее связь с другими параметрами вещества

Из зонной теории следует, что величина E_g твердых тел определяется химическим составом отклонением от стехиометрии и агрегатным состоянием соединения, кристаллической и дефектной структурой образца. Величина E_g зависит от температуры, давления, электрических, магнитных, гравитационных полей и других внешних параметров [1-11]. Для описания указанных зависимостей обычно используют линейные коэффициенты (например, температурный - α_T = δE_g/dT и барический - α_P = δE_g/dP, здесь T и P - абсолютная температура и гидростатическое давление), в ряде случаев (например, при фазовых переходах) могут потребоваться коэффициенты более высокого порядка. При изменении состава, отклонения от стехиометрии (фазы переменного состава), а также ряда внешних параметров (температуры, давления и др.) в кристаллах могут наблюдаться как структурные, так и чисто электронные фазовые переходы типа полупроводник-диэлектрик, либо полупроводник-металл, связанные с изменением E_g. [12]. Изменение E_g при фазовых переходах описывается соотношением:

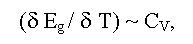
(здесь C_v - теплоемкость при постоянном объеме), соответственно E_g подобно C_v испытывает скачки при фазовых переходах I рода и точки перегиба для фазовых переходов II рода [17].

По величине E_g можно судить о типе химической связи, доминирующей в соединении, устойчивости соединения в определенном интервале изменений состава и внешних параметров, типе электронной проводимости в образцах, склонности материала к ионной проводимости, а также основных термодинамических характеристиках соединения (энтальпии образования H_F, энтропии ΔS_m и температуры плавления T_m и других) [13].

Методы определения ширины запрещенной зоны E_g

В настоящее время экспериментальные и теоретические методы исследования зонной структуры твердых тел охватывают интервал энергий до ~25 eV [16]. Для теоретических расчетов зонной структуры используют методы квантовой теории (линейной комбинации атомных орбиталей, ортогонализированных плоских волн, псевдопотенциала и др.). Точность теоретических расчетов E_g обычно не превышает ~0.5 eV. Последняя, однако, может быть повышена путем использования в теоретических расчетах опорных экспериментальных точек [16]. Сейчас для многих твердых тел достигнуто хорошее качественное понимание зонной картины в довольно большом интервале энергий, а в ряде случаев и полуколичественное знание зонных структур в интервале 10- 20 eV, где точность может достигать 0.5- 1.0 eV, то есть 5- 10 % [16]. В то же время, теоретические расчеты зонной структуры твердых тел все еще слишком грубы, чтобы однозначно интерпретировать, например, спектры электроотражения (экспериментальное разрешение спектральных пиков превышает ~0.01-0.001 eV) или предсказать величины зазоров между экстремумами валентной зоны и зоны проводимости, где требуется точность более ~0.1 eV [16]. Поэтому для достоверного определения E_g используют экспериментальные методы исследований, точность которых достигает ~0.1 eV (иногда до ~0.01 eV) [15,16].

Экспериментально величина E_g определяется из анализа различных физических эффектов, связанных с переходами электронов из зоны проводимости в валентную зону под действием термической активации (E_g^term), либо квантов света (E_g^opt). Обычно E_g^term определяют по температурному ходу электросопротивления и/или коэффициента Холла R в области собственной проводимости, а E_g^opt - из края полосы поглощения и длинноволновой границы фотопроводимости (Photo). Величину E_g можно оценить также из измерений магнитной восприимчивости, теплопроводности (биполярная компонента), опытов по туннелированию при низкой температуре и т.п. [15]. Существуют также некоторые эмпирические соотношения для качественной оценки ширины запрещенной зоны E_g материалов, например:

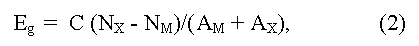
(здесь N_{X, M} и A_{X, M} - число и атомные номера валентных электронов аниона и катиона, С = 43 - постоянная), имеющие вспомогательный характер [14]. Применяется также оценка E_g методом экстраполяции (обычно линейной или квадратичной) в гомологических рядах известных соединений, либо фаз переменного состава [17].

Наиболее часто E_g определяют экспериментально по температурному ходу электросопротивления:

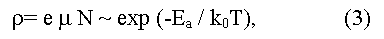
здесь e - заряд электрона, μ - подвижность электронов, в области собственной проводимости кристалла, когда концентрация носителей тока в зоне проводимости возрастает с температурой в результате термической активации по экспоненциальному закону:

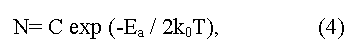
здесь С- константа, зависящая от параметров зон проводимости и валентной, k_o - постоянная Больцмана, T - абсолютная температура, E_a = (E_g/2) - энергия активации (коэффициент 1/2 показывает, что уровень Ферми должен быть расположен посередине запрещенной зоны). Метод требует учета температурной зависимости подвижности электронов μ.

Величину E_g определяют также путем измерения зависимости коэффициента Холла от температуры в области собственной проводимости по формуле [15]:

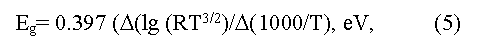
где R- коэффициент Холла, T- абсолютная температура.

Основные ошибки определения E_g указанными методами связаны c: 1) недостижением области собственной проводимости, влиянием активации примесных уровней и вкладом примесной проводимости; 2) неучетом температурной зависимости подвижности μ в формуле (3); 3) недостаточной протяженностью использованного интервала температур ΔT; 4) изменением химического состава образцов и протяженности области гомогенности соединений при высокой температуре и другими факторами [4,14,15].

Определение E_g из края собственного поглощения света полупроводником и фотопроводимости основано на возбуждении валентного электрона в зону проводимости за счет поглощаемой энергии фотона. Возможны прямые (вертикальные) оптические переходы (k₂ = k₁ + g, или k₂ ~ k₁, здесь k₁ и k₂ - волновой вектор электрона в конечном и исходном состоянии, g - волновой вектор фонона) и непрямые (невертикальные) оптические переходы с участием фононов ((k₂ ~ k₁+ K_ph, здесь K_ph - импульс фонона). Край собственного поглощения определяется при прямых и непрямых переходах соответственно соотношениями:

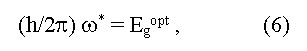
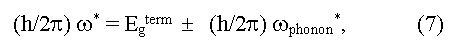
здесь ω* - граничная частота поглощения фотонов, ω_phonon - частота поглощаемого (+) и испускаемого (-) фонона, E_g^opt и E_g^term - оптическая и термическая ширина запрещенной зоны. Из выражений (6) и (7) следует, что величина E_g^opt = E_g^term для случая прямых вертикальных оптических переходов, в случае непрямых оптических переходов величина E_g^opt может быть как меньше (случай поглощения фонона), так и больше (случай испускания фонона) минимального расстояния между валентной зоной и зоной проводимости (E_g^term = E_g), причем измеренные значения E_g^opt могут существенно зависеть от кристаллографического направления в образце [5]. Обычно E_g^opt = E_g^term в ковалентных кристаллах, E_g^opt > E_g^term в ионных кристаллах, E_g^opt < E_g^term в случае экситонного поглощения света (образования связанных электрона и дырки). Экситонная ширина запрещенной зоны рассчитывается из соотношения:

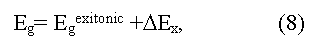
где ΔE_X - энергия связи экситона (eV)), в отдельных случаях измеренные значения E_g^opt и E_g^term могут различаться в несколько раз [14]. Указанные соотношения (6) и (7) верны для случая нахождения уровня Ферми в запрещенной зоне кристалла. В сильно легированных полупроводниках р-типа (полуметаллах) возбуждение электронов в зону проводимости происходит с уровня Ферми, расположенного в валентной зоне соединения, при этом величина E_g^opt. дополнительно увеличится до E_g^opt ~ E_g^term + E_F.

Заключение

Таким образом, величина E_g^term (в дальнейшем именуемая просто E_g - ширина запрещенной зоны) представляет собой не зависящую от кристаллографического направления истинную, или фундаментальную ширину запрещенной зоны кристалла, которая ответственна за все физические и физико-химические процессы, связанные с термической активацией носителей тока в образцах. В то же время, величина E_g^opt хотя и связана с E_g^term, однако имеет несколько меньшую общность и описывает оптические переходы электронов в кристаллах при определенной условиях эксперимента (кристаллографического направления, частоты и поляризации оптических фононов т.п.). Отсюда следует, что о достоверном знании величины E_g можно говорить только для всесторонне исследованных материалов.

Все указанные выше соображения учитывались при составлении настоящей базы данных, охватывающей значения ширины запрещенной зоны E_g основных неорганических веществ. Специально отмечены приводимые оригинальными авторами значения E_g, полученные из оптических, термических и электрофизических измерений. Приведены сопутствующие данные по химическому и фазовому составу материалов, типу кристаллической решетки (система, структурный тип, пространственная группа), указана ориентации образцов и температура измерений. Все приведенные данные соответствуют нормальному атмосферному давлению, а также отсутствию заметных электрических и магнитных полей.

Использованы следующие обозначения:

• ΔE, E_g - ширина запрещенной зоны (bandgap);
• Optical - величина определена из оптических данных;
• Thermal - величина определена по термической активации проводимости;
• Electrical - величина определена из электрофизических измерений;
• Photo. - величина определения из фотопроводимости;
• Exciton - экситонный;
• Calculation - расчет;
• Estimation - оценка;
• Theoretical - теоретическая оценка;
• h.t. - высокотемпературный;
• RT - комнатнотемпературный;
• l.t. - низкотемпературный;
• KI, KII, KIII - различные полиморфные модификации;
• (.) X, (.) Γ - различные точки зоны Бриллюена;
• Direct - прямой переход;
• Indirect - непрямой переход;
• (//a, b, c), (E//a, b, c) или (A, B, C) - вектор электрического поля поляризованной световой волны параллелен кристаллографическим осям a, b, c образца;
• (|− a, b, c), or (E |− a, b, c) - вектор электрического поля поляризованной световой волны параллелен кристаллографическим осям a, b, c образца соответственно.

Литература:

[1] Wilson A.H. The Theory of Metals, Cambridge, 1953.

[2] Peiers R.E. Quantum Theory of Solids, Oxford, 1953.

[3] Ziman J.M. Electrons and Phonons, Oxford, 1960.

[4] Kittel C. Quantum Theory of Solids, New York, 1963.

[5] Blatt F.J. Physics of Electronic Conduction in Solids, New York, 1968.

[6] Harrison W.A. Solid State Theory, New York, 1970.

[7] Lovett D. Semimetals and Narrow Bandgap Semiconductors, London, 1977.

[8] Mott N.F., Davis E.A. Electron Processes in Non-crystalline Materials, Oxford, 1979.

[9] Amorphous Semiconductors, Ed. Brodsky M.H., Berlin, 1979.

[10] Cutler M. Liquid Semiconductors, New York, 1977.

[11] Kao K., Hwang W. Electrical Transport in Solids, Oxford, 1979.

[12] Mott N.F.Metal-Insulator Transitions, London, 1979.

[13] Regel A.R., Glazov B.M. Periodical Law and Physical Properties of Electronic Melts, Moscow, 1978 (in Russian).

[14] Ormont B.F. Introduction to Physical Chemistry and Crystall Chemistry of Semicon-ductors, Moscow, 1973 (in Russian).

[15] Bush G, Vinkler U. Bestimmung der Charakteristischen Grossen Eines Halbleiters, Er-gebnisse der Exakten Naturwissenschaften, Bd.29, 145, 1956.

[16] Tsidilkovskiy I.M. Band Structure of Semiconductors, Moscow, Nauka, 1978 (in Rus-sian).

[17] Fridkin B.M. Ferroelectrics-semiconductors, Moscow, Nauka, 1976 (in Russian).

[18] Bugaev A.A., Zaharchenia B.P., Chudnovskiy F.A. Insulator to Metall Phase Transition and its Applications, Leningrad: Nauka, 1979, 183 pp. (in Russian).

К.ф.-м.н. М.А.Коржуев (ИМЕТ РАН)

English